Today's Goals
1. 다시 학습 주간에 익숙해지기 - 코드카타 SQL & 파이썬
2. 통계학...이걸 내가 또 배울 줄이야
갑자기 학문적인? 공부를 다시 시작하니 정신이 없다ㅏㅏ아아
내 뇌가 대학교때로 돌아가면 얼마나 조아
1. 코드카타
SQL
[잊고 있던 substr & concat]
- substr : 원하는 위치의 문자를 원하는 만큼 가져오는 것 > substr(컬럼, 시작 위치, 가져올 개수)
- 파이썬만 쓰다보니 문자를 합할 때 + 를 쓰려고.....
- SQL에서 문자 연결은 concat으로
[SQL의 cross join]
- 따로 join없이 from table1, table2 로 표시하면 cross join의 의미
[SQL에서 delete 사용하기]
delete a
from Person a join Person b on a.email = b.email
where a.id > b.id- 위 쿼리에서 delete는 조건에 해당하는 행을 삭제한 결과를 반환해줌
- 명시적으로 삭제가 일어난 a 테이블에 대해서만 결과가 출력됨
- 즉, 위 쿼리는 기존 테이블 a에서 조건에 해당하는 행과 같은 행이 제거되며, 제거된 후의 테이블 a를 출력함
파이썬
[numpy 없이 행렬 배열에 접근하기]
def solution(arr1, arr2):
for i in range(len(arr1)) :
for j in range(len(arr1[0])) :
arr1[i][j] += arr2[i][j]
return arr1- 2차원 배열은 [행][열]로 표현, 즉, 배열에서 행이 먼저 읽힘
- 따라서 행렬 배열 자체의 길이를 구하면 행의 개수, 행렬 배열의 한 행을 불러와서 길이를 구하면 열의 개수
프로그래머스 | 행렬의 덧셈 [파이썬 python]
프로그래머스 코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요. programmers.co.kr 코드 def
dduniverse.tistory.com
[strip()]
- strip은 문자열의 선행과 후행에서 특정 문자 혹은 공백을 제거하여 문자열의 복사본을 반환함
a, b = map(int, input().strip().split(' '))- 따라서 위 코드의 의미는, 사용자가 한줄로 입력한 두개의 숫자를 받아서, 앞뒤 공백을 제거하고, 띄어쓰기를 기준으로 나누어, 각각 정수로 변환하여 a와 b에 저장하는 것
- strip('w') 이렇게 입력하면 선행과 후행에서 w가 아닌 값이 나올때까지 계속 제거함
- 입력되는 문자의 모든 조합에 대해 적용됨(strip('abc') 하면 선행과 후행에서 a or b or c 중에 아무것도 없을때 까지)
- 아래 예제 꼭 확인
strip()_ 문자열 및 공백 제거
### 선행과 후행 문자가 제거된 문자열의 복사본을 돌려줍니다. chars 인자는 제거할 문자 집합을 지정하는 문자열입니다. 생략되거나 None 이라면, chars 인자의 기본값…
wikidocs.net
[* 모양으로 꽉 찬 사각형 그리기]
for i in range(b) :
print('*' * a)- 파이썬의 배열은 행>열 이었던 것을 기억하면서 가로 길이 세로 길이의 순서를 중요하게 볼 것(아래 블로그의 다른 풀이 참고)
https://wackylife.tistory.com/71
[프로그래머스/Level1/파이썬3] 직사각형 별찍기
코딩테스트 연습 - 직사각형 별찍기 이 문제에는 표준 입력으로 두 개의 정수 n과 m이 주어집니다. 별(*) 문자를 이용해 가로의 길이가 n, 세로의 길이가 m인 직사각형 형태를 출력해보세요. 제한
wackylife.tistory.com
2. 통계학
라이브 세션
[모집단과 표본집단]
- 모집단에서 표본을 추출(sampling), 표본집단을 이용해 모집단을 추정
[추론통계의 기반은 분포, 가장 많은 기반이 되는 것은 정규분포]
[분포란 무엇인가]
- 특정 값을 중심으로 다른 값들이 흩어진 형태
- 이산확률분포와 연속확률분포로 분류할 수 있음

[베르누이 분포]
- 확률 변수의 경우가 2가지인 경우(예 : 동전, 클릭 > 한다 안한다 된다 안된다)

[이항 분포]
- 베르누이 분포에서 시행 횟수가 추가되는 것(사건 발생의 경우의 수까지 확장)


- 시행 횟수(n)이 매우 커지면 정규분포와 비슷해짐
[균등 분포]
- 연속확률분포 중 하나로, 모든 x에 대해 확률이 동일한 분포
[정규 분포]
- 평균을 기준으로 좌우 대칭, 봉우리 1개, 연속확률분포
- 정규분포의 평균과 표준편차를 안다면 특정 데이터가 전체 데이터의 몇%에 포함되는지 알 수 있음

[왜도와 첨도]
- 왜도는 확률의 비대칭 정도(왼쪽으로 기울었는지, 오른쪽으로 기울었는지, 긴꼬리 분포라고도 부름)

- 첨도는 뾰족한 정도(정규분포보다 둥글면 이상치 적음, 정규분포보다 뾰족하면 이상치 많음)

[표준 정규 분포]
- 평균 0, 표준편차 1인 정규분포 (정규분포인 데이터에 대해서 정규화를 수행한 것)
- z값 : 그래프 상에서 마이너스 극한에서부터 해당하는 z값 까지 누적된 확률을 알 수 있음

- 정규분포를 따르는 데이터에서 평균과 표준편차를 안다면 특정 값(X)가 백분율 몇%, 즉 상위 몇%인지 알 수 있음
[정규분표로 힘들게 계산하지말고, Scipy를 쓰자]
- Scipy는 기초통계 모듈과 함수를 모아놓은 라이브러리
scipy
│
├── stats # 통계 분석과 확률 분포 관련 함수 제공
│ ├── norm # 정규분포 관련 함수 (PDF, CDF, 랜덤 샘플링 등)
| |── uniform # 균등분포
| |── bernoulli # 베르누이 분포
| |── binom # 이항분포
│ ├── ttest_ind # 독립 두 표본에 대한 t-검정
│ ├── ttest_rel # 대응표본 t-검정
│ ├── mannwhitneyu # Mann-Whitney U 비모수 검정
│ ├── chi2_contingency # 카이제곱 독립성 검정
│ ├── shapiro # Shapiro-Wilk 정규성 검정
│ ├── kstest # Kolmogorov-Smirnov 검정 (분포 적합성 검정)
│ ├── probplot # Q-Q plot 생성 (정규성 시각화)
│ ├── pearsonr # Pearson 상관계수 계산
│ ├── spearmanr # Spearman 순위 상관계수 계산
│ └── describe # 기술 통계량 제공 (평균, 표준편차 등)- scipy.stats.분포이름.메서드 라는 규칙을 따라 사용
- 메서드는 아래 이미지 참고


기초 강의
[표본오차와 신뢰구간]
- 표본오차는 표본의 통계량과 모집단의 진짜 값의 차이 > 표본이 클수록 표본오차가 작아짐
- 신뢰구간은 모집단에 대해 추정된 값이 포함될 것으로 기대되는(예측되는) 범위
- 신뢰구간=표본평균±z×표준오차 (예 : 95% 신뢰수준의 z값은 1.96)
[긴 꼬리 분포]
- 데이터가 비대칭적으로 꼬리 형태로 분포할 때 사용

- 일부가 전체적으로 큰 영향을 미치는 사례에서 사용됨(일부 부유층의 비중이 큰 소득, 소수 인기 제품의 판매량이 많은 온라인 쇼핑 등)
[스튜던트t 분포]
- 자유도가 커질수록 정규분포에 가까워지는 것으로, 자유도란 표본의 크기와 관련 있음

- 모집단의 표준편차를 알 수 없고, 표본의 크기가 작은(보통 30미만) 경우 정규분표 대신 사용(소규모 임상 시험에서 두 그룹 간의 차이 분석과 같은 약물 시험)
[카이제곱분포]
- 범주형 데이터의 독립성 검정이나 적합도 검정에 사용되는 분포
- 독립성 검정은 두 범주형 변수간의 관계가 있는지 확인하는 것
- 적합도 검정은 관측값들이 특정 분포에 해당하는지 검정하는 것

- k는 자유도이며, 원인이 되는 독립변수들이 완벽하게 서로 다른 질적 자료일 때 (성별이나 나이에 따른 선거 지지율)
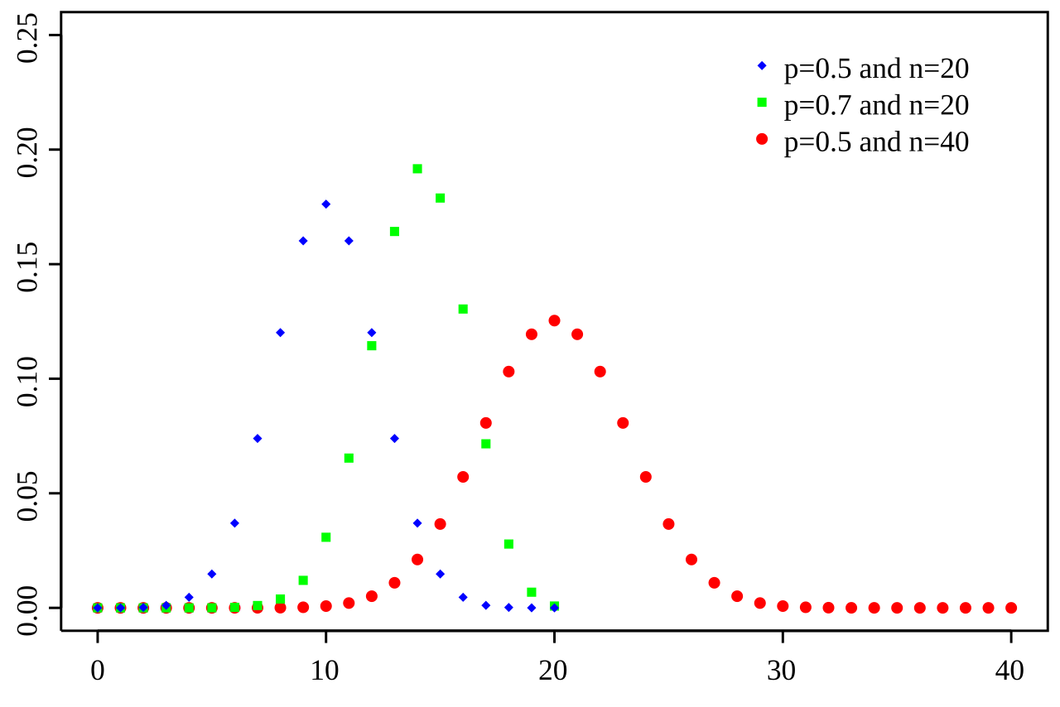
[이항분포]
- 두가지 결과를 가지는 실험을 여러번 반복했을 때 성공 횟수의 분포(연속된 값을 가지지 않고 특정 정수값만 가짐)
- 불량품 모니터링에서 표본집단의 불량품 수의 분포
[푸아송 분포]
- 단위 시간 또는 단위 면적당 희귀한 사건이 발생할 때 사용하는 분포(특정 시간동안 콜센터 전화 수, 특정 도로 구간에서 일정 기간동안 발생하는 교통사고 수)

- 연속된 값을 가지지 않는 이산형 분포에 해당됨
- 평균 발생률 λ(주어진 시간이나 공간에서 사건이 몇번 발생했는가)가 충분히 크다면 정규분포와 비슷해짐
[분포 선택 방법]

'데이터 부트캠프 - Today I Learned' 카테고리의 다른 글
| [스파르타 내일배움캠프 / 데이터 분석 트랙] TIL(Today I Learned)_7주차_25.01.09 (0) | 2025.01.09 |
|---|---|
| [스파르타 내일배움캠프 / 데이터 분석 트랙] TIL(Today I Learned)_7주차_25.01.08 (0) | 2025.01.08 |
| [스파르타 내일배움캠프 / 데이터 분석 트랙] TIL(Today I Learned)_7주차_25.01.06 (0) | 2025.01.06 |
| [스파르타 내일배움캠프 / 데이터 분석 트랙] WIL(Weekly I Learned)_6주차 (0) | 2025.01.05 |
| [스파르타 내일배움캠프 / 데이터 분석 트랙] TIL(Today I Learned)_6주차_25.01.03 (1) | 2025.01.03 |